We often discuss the benefits of diversification when it comes to investing and constructing a portfolio. However, in conversations with clients I often find there are widespread misconceptions about why diversification is desirable, how to achieve effective diversification, how diversification can be measured, as well as some of the obvious implications of having a well-diversified portfolio. In this series of blog posts, I hope to address each of these items.
Let’s start with asking the obvious question; why is a diversified portfolio desirable? The simple answer is if we knew how the future was going to play out we would simply pick the winning investment(s) ahead of time and be done with it. For example, if you knew which team would win the Super Bowl then a rational decision would be to bet your entire net worth plus whatever you could borrow on that team. Even then, though, there is a hidden risk, right? What if our counterparty (the loser) can’t or won’t pay us when our team wins? We seek to diversify since the future is uncertain. The more uncertain or the more fragile the global capital markets are the more we should consider diversification as one of our primary objectives especially if we have already accumulated a significant next egg. We need to continue to grow it, but we can’t afford to take massive losses going forward.
OK, if diversification is good since the future is always uncertain then what exactly are we attempting to diversify? The answer again is simple but powerful. We want to diversify our risk exposure. Since the future is always uncertain and all investments have risk(s) we want separate elements of our portfolio to be exposed to different risk factors. You are undoubtedly aware that high quality bonds have historically been a very good diversification vehicle relative to stocks. Why? Well stock price is typically correlated to earnings over the long term but in the short term it can be influenced greatly by events specific to that company, other companies in the same industry or the direction of the general market. High quality bond prices, on the other hand, are most impacted by changes in interest rates. At a more elemental level, stocks are a risk seeking investment whereas bonds are designed to be a safe place to park one’s capital. Those are fundamentally different risk postures; return on capital vs. return of capital. It makes intuitive sense that in a strong economy folks become more risk seeking and are more eager to invest in stocks in the expectation of high future returns whereas in a poor economy the safe harbor aspect of bonds may be more appealing. Therefore, it should not be surprising to observe that stock and bond prices often move in opposite directions. In other words, bonds have historically offered excellent diversification from stock primarily because they are subject to very different primary risk factors.
How do we measure diversification? To simplify the concept let’s take two variables (x and y) which could represent the prices of two different investments over some period. If we plot x vs y on a graph what do we see? If x and y are strongly correlated then we observe a set of points that fall very close to an upward sloping straight line. If x and y are negatively correlated the points define a line with a downward slope. If there is no correlation between x and y the data points look like a shotgun blast. Weak to moderate correlations are manifested as ovular groupings of the data as an uncorrelated circle of data points transitions to a clear linear pattern. By using some math, which we will avoid, we can quantify how well correlated the x values are to the y values. This is called the Correlation Coefficient or R for shorthand. If x and y are perfectly correlated then R = +1, if they are perfectly correlated but x increases as y decreases then R = -1. If there is no correlation whatsoever between x and y then R = 0. The graphic below provides a visual representation of data sets whose correlation coefficient varies between minus one and plus one.
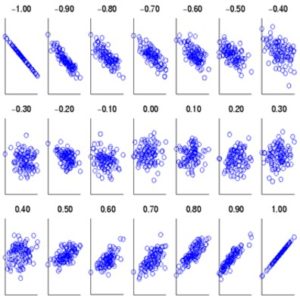
One other important feature of the correlation coefficient, R, is that it has a very useful physical interpretation between the relationship of y to x. The quantity R2, (often described as “R squared”) tells us how much of the value of Y is dependent on the value of X. For example, if r = 0.922 (highly correlated) then R2 = 0.85 which means that 85% of the value of Y is determined by the value of X while the other 15% of the value of Y has nothing to do with the value of X. Now substitute “investment 1” for “X” and “investment 2” for “Y” and it becomes readily apparent how one can quantify the degree of diversification between investment 1 and investment 2. Specifically, an absolute value of R, |R|, of 0.4 or less means the investments are well diversified, |R| of 0.7 or greater means the investments are highly correlated (not diversified) and values in between suggest moderate correlation and diversification. Going back to our hypothetical example of an R2 0f 0.85 those two investments are highly correlated and thus do not provide meaningful diversification relative to one another. They tend to move in lockstep with one another. This is great if X is increasing in price but no investment only goes up, right?
One final important implication until next time. We obviously desire all elements of our portfolio to increase in value over our holding period which is typically many years or at least a full market cycle. However in a well diversified portfolio we should expect that at any point in time there are some elements actually declining in price. Simply because an investment is declining in price doesn’t imply it is a bad investment. In fact, if we observe that all elements are going up at the same time rather than rejoicing maybe we should take a closer look at our holdings. We may realize that we haven’t adequately diversified our risks!